ЭММ : 1.Задачи Линейного программирования. Геометрическая интерпретация. Симплексный метод

Линейные модели являются одним из наиболее активно используемых классов мат. моделей. Они сравнительно просты и хорошо разработаны и достаточно эффективны в целом ряде стандартных ситуаций.

Программирование в данном термине имеет смысл планирования, а линейное означает, что ищется экстремум линейной целевой функции при линейных ограничениях.

Наиболее часто и эффективно ЛП применяется при решении следующих типов задач:

• задачи о составлении смеси, цель — в выборе наиболее экономичной смеси ингредиентов
• задачи производства, цель — подбор наиболее выгодной производственной программы выпуска продукции при использовании ограниченных ресурсов
• задачи распределения: организация доставки материалов от определенного числа источников к определенному числу потребителей с минимизацией расходов на доставку,

Построение математической модели включает 3 этапа:

1. определение переменных
2. выбор целевой функции
3. наложение ограничений

Переменными называются величины х1, х2, …,хn, кот. полностью характеризуют экономический процесс. Их можно записать в виде вектора х = (х1, х2, …,хn).

Целевой функцией называется функция переменных задачи, кот. характеризуют качество выполняемой задачи и экстремум, кот. необходимо найти. Для ЗЛП целевая функция линейна и в общем виде выглядит так:

Z (x)=c1×1+c2×2+…+cnxn -> max (min)

Система ограничений включает в себя систему уравнений и неравенств, кот. удовлетворяют переменным задачи и кот. следуют из ограниченности ресурсов или других экономических и физических условий. В общем виде выглядит как:

a₁₁x₁ + a₁₂x₂ + a₁₃x₃ + … + a_1nx_n <= b₁
a₂₁x₁ + a₂₂x₂ + a₂₃x₃ + … + a_2nx_n <= b₂
……………………………………………..
a_m1x₁ + a_m2x₂ + a_m3x₃ + … + a_mnx_n <= b_m
xi>0, i =1,n

Линейность предполагает наличие 2-х свойств: пропорциональности и аддитивности. Пропорциональность означает, что вклад каждой переменной в целевую функцию и в левые части ограничений прямо пропорционален величине этой переменной. Аддитивность заключается в том, что целевая ф-я представляет собой сумму вкладов различных переменных.

Для того, чтобы решить задачу, необходимо привести ее к стандартному либо каноническому виду.

Стандартный вид ЗЛП — задача на максимум при ограничении типа ≤ (на минимум при ≥), на все переменные наложены условия неотрицательности. Если в задаче есть уравнения, то чтобы их привести к виду ≤, необходимо из левой части вычесть переменную xn+1, если ограничение ≥, то умножить на -1. Если не на все переменные наложено условие неотрицательности, необходимо заменить переменную разностью 2х неотрицательных переменных xt = xn+2 — xn+3

Графическая интерпретация.

1. Построить область допустимых решений, в которых одновременно удовлетворяются все ограничения
2. На график наносят ряд параллельных прямых, соответствующих уравнению целевой функции при нескольких произвольно выбранных и последовательно возрастающих значениях целевой функции.
3. Определяется наклон целевой функции направление, в котором происходит увеличение.
4. Перемещаем прямую целевой функции в направлении возрастания до тех пор, пока она не сместиться в область недопустимых решений.
5. Определим последнюю точку касания прямой и допустимой области решения. Находим координаты этой точки, решая систему двух уравнений, на пересечении которых лежит данная точка.
6. Вычисляем значения целевой функции в этой точке.

Пример:
Z = 4×1 — 3×2 ->ecstr
-x1 + 2×2<=14
2×1 + x2<=17
3×1 — x2<=8
X1 + x2 =>4
X1>0
X2>0
Ответ: F (a)min = -21, F (b)max = 9

Вывод:

• если оптимальный план существует, то он находится не внутри, а на границе многоугольника решений.
• если оптимальный план единственный, то он совпадает с одной из угловых точек многоугольника решений.
• если оптимальных планов множество, то они совпадают с одной из сторон многоугольника решений.
• если оптимальный план не существует, то система неравенств противоречива или определена неограниченным прямоугольником вершины.

Симлекс-метод.

Разработан в 1947 г. Американским ученым Данцингом. В настоящее время симплекс метод является универсальным методом линейного программирования.

При графическом способе решения ЗЛП решению всегда соответствует одна из угловых точек пространства решения. Именно этот результат положен в основу решения симплекс методом. В его вычислительной схеме реализуется упорядоченный процесс, при кот., начиная с некоторой исходной угловой точки (обычно (0,0)), осуществляют последовательные переходы от одной экстремальной точки к другой до тех пор, пока не будет найдена точка, соответствующая оптимальному решению.

Решение, найденное в точке (0,0) называется начальным решением. От этой точки происходит переход к некоторой смежной угловой точке. Выбор точки зависит от коэффициентов ЦФ. Выбор последующей точки определяется двумя правилами:

1) каждая последующая угловая точка должна быть смежной с предыдущей.
2) обратный переход, предшествующий экстремуму точки производиться не может.

Будем считать, что линейная модель канонической формы содержит m уравнений и n неизвестных, где m≤n, тогда все допустимые экстремальные точки определяются как все однозначные неотрицательные решения системы m уравнений, в которой n-m переменных приравниваются к 0. Однозначность такой Си уравнений называется базисным решением.

Если базисное решение удовлетворяет требованию неотрицательности правых частей, то оно называется допустимым базисным решением. Переменные, имеющие 0-е значение явл. небазисными, остальные — базисными.

Реализация вычислений процедур симплекс методом существенно упрощается тем, что для каждую последующую экстремальную точку можно найти путем взаимной замены по одной переменной в составе базисных и небаз. переем-х.

Включаемой переменной называется небазисная в данный момент переменная, кот. будет включена в множество базисных переменных на следующей итерации.

Исключаемая переменная — это та базисная переменная, кот. на следующей итерации подлежит исключению из множества базисных переменных.

Алгоритм симплекс-метода.

Шаг 0. Используя линейную модель канонической формы определяют начальной допустимое базисное решение путем приравнивая к 0 n-m небазисных переменных.

Шаг 1. из числа текущих небазисных, приведенных к 0 переменных, выбирается включаемая в новый базис переменная, увеличение которой обеспечивает улучшение значений ЦФ. Если такое переменной нет, то вычисления прекращаются, т. к. текущее базисное решение — оптимальное. В противном случае переход к шагу 2.

Шаг2. Из числа переменных текущего базиса выбирается исключаемая переменная, кот. должна принять нулевое значение при введении в состав базиса новой переем.

Шаг 3. Находится новое базисное решение, соответствующее новому составу базисных и небазисных переем-х. Далее снова шаг 1.

Существуют два условия, используемые в симплекс методе:

• Условие оптимальности: вводимой переменной в задаче на max является небазисная переменная, имеющая в Z-уравнении наибольший по модулю отрицательный коэффициент. В случае равенства таких коэффициентов для нескольких небазисных переменных, выбор делается произвольно. Если все коэффициенты при небазисных переменных в Z-уравнении неотрицательны, то получаемое решение — оптимальное. Симплекс-столбец, ассоциированный с вводимой переменной называется ведущим, или разрешающим.
• Условие допустимости: в задачах на max в качестве исключаемой выбирается та базисная переменная, для которой отношение постоянной правой части соответствующего ограничения к положительному коэффициенту ведущего столбца минимально. В случае равенства этого отношения для нескольких базисных переменных, выбор делается произвольно.

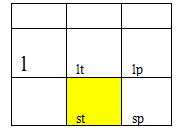
Строку соответствующую исключаемой переменной называют ведущей, или разрешающей.

Элемент, находящийся на пересечении ведущих столбца и строки, называется ведущим элементом.

a_st -ведущий столбец текущей таблицы
a^’_{st –} рассчитываемы элемент новой симплекc-таблицы
a^’_st=(a_lp*a_st- a_lt* a_sp)/ a_st

Пример

Для изготовления 4 видов продукции требуется 3 вида сырья. Запасы и нормы представлены в таблице.

Найти max общей стоимости выпускаемой продукции.

Z = 12×1 + 7×2 + 18×3 + 10×4 -> max
x1 + 2×2 + x3 <=18
x1 + x2 + 2×3 + x4 <= 30
x1 + 3×2 + 3×3 + 2×4 <=40
xi => 0, i = 1,4

x1 + 2×2 + x3 + x5 <=18
x1 + x2 + 2×3 + x4 + x6 <= 30
x1 + 3×2 + 3×3 + 2×4 + x7<=40
xi => 0, i = 1,7
Z = 12×1 + 7×2 + 18×3 + 10×4 + x5 + x6 + x7 -> max

x5 = 18 — (x1 + 2×2 + x3)
x6 = 30 — (x1 + x2 + 2×3 + x4)
x7 = 40 — (x1 + 3×2 + 3×3 + 2×4)

x1 = x2 = x3 = x4 = 0

x5 = 18
x6 = 30
x7 = 40
Z = 0

Если в ведущей строке есть 0, то столбцы, переносятся в следующую таблицу без изменений и, наоборот, если в столбце есть 0, то строки переносятся.

Остальные элементы считаются по правилу прямоугольника.

Напрмер:
A51 = (1 * 3 — 1 * 1) / 3 = 2/3
A52 = (2 * 3 — 1 * 3) / 3 = 1 и т. д.

Вычисления продолжаются до тех пор, пока в строке Z все элементы не будут положительными.