Эконометрика : 1.Спецификация экономических моделей

Парная линейная регрессия

Линейная регрессия (теоретическое линейное уравнение регрессии) представляет собой линейную функцию между условным математическим ожиданием М (Y;X=x_i) зависимой переменной Y и одной объясняющей переменной X (x_i — значения независимой переменной в i-ом наблюдении, i = l, 2, …, n).

М (Y;X=x_i) = betta₀ + betta₁x_i. (3.5)

Для отражения того факта, что каждое индивидуальное значение y_i отклоняется от соответствующего условного математического ожидания, необходимо ввести в соотношение (3.5) случайное слагаемое epsilon_i,

y_i = М (Y;X=x_i) + epsilon_i = betta₀ + betta₁x_i+ epsilon_i. (3.6)

Соотношение (3.6) называется теоретической линейной регрессионной моделью; betta₀ и betta₁ — теоретическими параметрами (теоретическими коэффициентами) регрессии; epsilon_i — случайным отклонением. Следовательно, индивидуальные значения y_i представляются в виде суммы двух компонент: систематической (betta₀ + betta₁x_i) и случайной (epsilon_i). В общем виде теоретическую линейную регрессионную модель будем представлять в виде

Y = betta₀ + betta₁X+ epsilon. (3.7)

Задачи линейного регрессионного анализа состоят в том, чтобы по имеющимся статистическим данным (x_i, у_i, i = 1, 2, …, n) для переменных X и Y: а) получить наилучшие оценки неизвестных параметров betta₀ и betta₁; б) проверить статистические гипотезы о параметрах модели; в) проверить, достаточно ли хорошо модель согласуется со статистическими данными (адекватность модели данным наблюдений). Следовательно, по выборке ограниченного объема мы сможем построить так называемое эмпирическое уравнение регрессии

y_теор(x_i) = a_* + b_*x_i, (3.8)

где y_теор(x_i) — оценка условного математического ожидания M (Y ÷ Х = x_i); a_* и b_* — оценки неизвестных параметров betta₀ и betta₁, называемые эмпирическими (выборочными) коэффициентами регрессии. Следовательно, в конкретном случае

y_i = a_* + b_*x_i+e_i, (3.9)

где отклонение e_i — оценка теоретического случайного отклонения epsilon_i.

Однако первая сумма не может быть мерой качества найденных оценок в силу того, что существует бесчисленное количество прямых (в частности, Y = у_ср), для которых SUMe_i = 0.

Метод определения оценок коэффициентов из условия минимизации второй суммы называется методом наименьших модулей (МНМ).

Самым распространенным и теоретически обоснованным является метод нахождения коэффициентов, при котором минимизируется третья сумма. Он получил название метод наименьших квадратов (МНК). Среди других методов определения оценок коэффициентов регрессии отметим метод моментов (ММ), метод максимального правдоподобия (ММП) и метод центра неопределённости (МЦН).

Парная нелинейная регрессия

Нелинейными оказываются производственные функции (зависимости между объемом произведенной продукции и основными факторами производства — трудом, капиталом и т. п.), функции спроса (зависимость между спросом на товары или услуги и их ценами или доходом) и др.

Могут использоваться как модели, не линейные по переменным, так и не линейные по параметрам.

Все нелинейные регрессии делятся на два класса:

1) регрессии, нелинейные по объясняющим переменным, но линейные по оцениваемым параметрам:

полиномы разных степеней

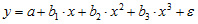
равносторонняя гипербола

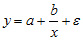
2) регрессии, нелинейные по оцениваемым параметрам:

степенная

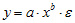
показательная

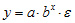
Экспоненциальная

Множественная регрессия

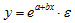
Множественная регрессия – это уравнение статистической связи с несколькими независимыми переменными:

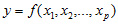(5.1)

где y — зависимая переменная (результативный признак);

x₁, x₂, …, x_p – независимые переменные (факторы). Все эти переменные входят в уравнение (5.1) с некоторыми коэффициентами.

Возможны разные виды уравнения множественной регрессии, чаще используются следующие функции: линейные и нелинейные.

В линейной множественной регрессии коэффициенты при х_i характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизменных значениях других факторов, закреплённых на среднем уровне.

При изучении вопросов потребления коэффициенты регрессии рассматриваются как характеристики предельной склонности к потреблению. Например, если функция потребления С_t имеет вид С_t = b₀ + b₁* R_t + b₂* R_t_-1 +epsilon_t, то потребление за t-й период времени зависит от дохода того же периода R_t и от дохода предшествующего периода R_t_-1. Соответственно, коэффициент b₁ характеризует эффект от единичного возрастания дохода R_t при неизменном уровне предыдущего дохода. Коэффициент b₁ обычно называют краткосрочной предельной склонностью к потреблению. Общим эффектом возрастания как текущего, так и предыдущего дохода будет рост потребления на величину b= b₁+b₂. Коэффициент b рассматривается здесь как долгосрочная предельная склонность к потреблению.

Функция потребления может рассматриваться также в зависимости от прошлых привычек потребления, т.е. от предыдущего уровня потребления C_t_-1:

С_t = b₀ + b₁R_t + b₂C_t-1 + e_t.

В этом уравнении параметр b₁ также характеризует краткосрочную предельную склонность к потреблению, т.е. влияние на потребление единичного роста доходов того же периода. Долгосрочная предельная склонность к потреблению имеет вид b₁/(1- b₂).

В степенной функции y_теор(x₁,x₂,…,x_p) = ax1^b1 x2^b2 …xp^bp коэффициенты b1, b2, …, bp являются коэффициентами эластичности. Они показывают, на сколько процентов изменяется в среднем результат с изменением соответствующего фактора на 1% при неизменности действия других факторов. Этот вид уравнения регрессии получил наибольшее распространение в производственных функциях, в исследованиях спроса и потребления.