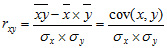 (1)
(1)Корреляция - вероятностная или статистическая зависимость, не имеющая строго функционального характера. В отличие от функциональной, корреляционная зависимость возникает тогда, когда один из признаков зависит не только от данного второго, но и от ряда случайных факторов или когда среди условий, от которых зависят и тот и другой признаки, имеются общие для них обоих условия. В случае корреляционной зависимости, изменение одной случайной величины приводят к изменению среднего значения другой случайной величины. Особенность корреляции состоит в том, что связи обнаруживаются не в единичных случаях, а в массовых явлениях, следовательно, необходимо иметь как можно больше объектов наблюдения.
Корреляция рассчитывается по формуле:
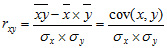 (1)
(1)
x - математическое ожидание х, - математическое ожидание y. (Математическое ожидание – среднее значение случай величины.)
cov (x,y) – ковариация переменных (ковариация определяет меру взаимодействия двух случайных переменных)
sigmax – стандартное отклонение x; sigmay – стандартное отклонение y
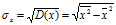
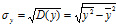 (2)
(2)
D(x) – дисперсия случайной величины х; D(y) – дисперсия случайной величины y. Дисперсия характеризует отклонение (разброс, рассеяние) значений случайной величины относительно среднего значения.
Формулу (1) можно представить в виде
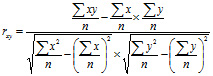 (3)
(3)
Коэффициенты корреляции бывают следующих видов:
1)парные коэффициенты корреляции
2)частные коэффициенты корреляции
3)коэффициенты множественной корреляции.
Парные коэффициенты корреляции используются для измерения тесноты связи между двумя переменными без учета их взаимодействия с другими переменными.
Например,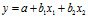
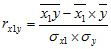
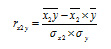
С помощью парного линейного коэффициента корреляции выявляется связь между двумя признаками, один из которых можно рассматривать как результативный, другой — как факторный. Но в действительности на результат воздействуют несколько факторов. В связи с этим возникают два типа задач: задачи измерения комплексного влияния на результативную переменную нескольких переменных и задачи определения тесноты связи между двумя переменными при фиксированных значениях остальных переменных. Задачи первого типа решаются с помощью множественных коэффициентов корреляции, задачи второго типа — с помощью частных коэффициентов корреляции.
Частный, или чистый, коэффициент корреляции между двумя признаками (х и y) при исключении влияния третьего признака (z) рассчитывается по формуле:
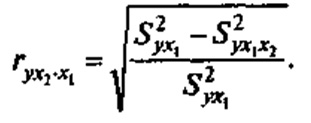
остаточная дисперсия(остаточная сумма квадратов) = S2
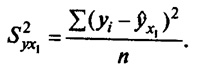
Если выразить остаточную дисперсию через показатель детерминации S2 остат = sigma2у*(1 - r2), то формула коэффициента частной корреляции примет вид:
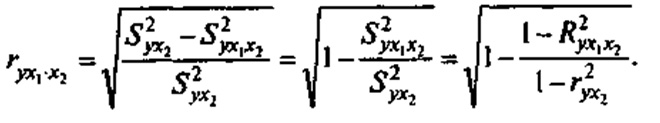
В зависимости от количества переменных, влияние которых исключается, частные коэффициенты корреляции могут быть различного порядка: y= a+b1*x1+ b2*x2+ b3*x3
Коэффициент частной корреляции, измеряющий влияние на у фактора хi, при неизменном уровне других факторов, можно определить по формуле
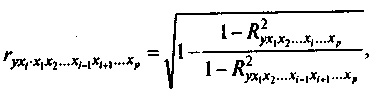
где R(верхнее) — множественный коэффициент детерминации всего комплекса р факторов с результатом y;
R(нижнее)— тот же показатель детерминации, но без введения в модель фактора xi.
Коэффициенты частной корреляции более высоких порядков можно определить через коэффициенты частной корреляции более низких порядков по рекуррентной формуле
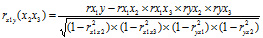
Парные и частные коэффициенты корреляции попадают в диапазон: -1≤rxy≤1
Если исследуется связь между несколькими переменными, то используется коэффициент множественной корреляции. Он означает: влияние (одновременное) факторных признаков x на результат:
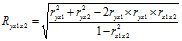
Множественный коэффициент корреляции изменяется в пределах от 0 до 1. Равенство нулю говорит об отсутствии линейной связи, равенство единице - о наличие тесной связи. Определить является ли связь прямой или обратной по данному коэффициенту нельзя.