Эконометрика : 3.Определение доверительных интервалов прогноза по линейному уравнению регрессии

Одной из центральных задач эконометрического моделирования является предсказание (прогнозирование) значений зависимой переменной при определенных значениях объясняющих переменных. Здесь возможен двоякий подход: либо предсказать условное математическое ожидание зависимой переменной при определенных значениях объясняющих переменных (предсказание среднего значения), либо прогнозировать некоторое конкретное значение зависимой переменной (предсказание конкретного значения).

Предсказание среднего значения. Пусть построено уравнение парной регрессии y_teor(x_i) = b₀ + b₁x_i, на основе которого необходимо предсказать условное математическое ожидание М(YiХ = х_p) переменной y_teor(x_p)  при X = х_p. В данном случае значение y_teor(x_p) = b₀ + b₁x_p является оценкой (приближением) М(YiХ = х_p).

Чтобы построить доверительный интервал, покажем, что случайная величина  y_teor(x_p)  имеет нормальное распределение с конкретными параметрами. имеем:

y_teor(x_p) = b₀ + b₁x_p = SUMd_i y_i +(SUM c_i y_i)x_p = SUM(d_i +c_ix_p)y_i.

Следовательно, y_teor(x_p) является линейной комбинацией нормальных случайных величин и, значит, сама имеет нормальное распределение.

My_teor(x_p) = M(b₀ + b₁x_p) = M(b₀)+ M(b₁)x_p = betta₀ + betta₁x_p

Dy_teor(x_p) = D(b₀ + b₁x_p) = D(b₀)+ D(b₁) +2cov(b₀ ,b₁)x_p (8.12)

(здесь используются формулы:
D(X+Y) = D(Х)+D(У)+ 2соv(Х, Y);
D(сХ) = с²D(Х);
cov(Х, bY) = bсоv(Х, Y))

cov(b₀ ,b₁) = M[(b₀ – M(b₀)(b₁ – M(b₁))] =

= M[(b₀ - betta₀)(b₁ – betta₁)] = M[((b₁ – M(b₁))] =

= - M[(b₁ - M(b₁)(b₁ – M(b₁))] =  M[(b₁ - betta₁)(b₁ – betta₁)] =

= -D(b₁) =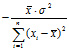

Следовательно

=

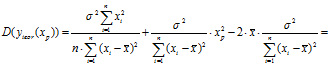
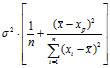
Так как

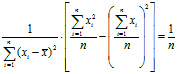
Поскольку

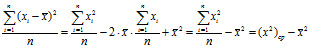
Подставив вместо sigma² её несмещенную оценку

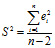
получим выборочную исправленную дисперсию D(y_teor(x_p)) рассматриваемой случайной величины.

Тогда случайная величина

имеет распределение Стьюдента с числом степеней свободы n = n–2. Следовательно, по таблице критических точек распределения Стьюдента по требуемому уровню значимости alfa и числу степеней свободы n=n–2 можно определить критическую точку t_alfa/2,n-2, удовлетворяющую условию Р(iТi < t_alfa/2,n-2) = 1–alfa.

имеем:

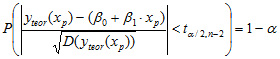
После алгебраических преобразований получим:

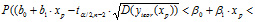
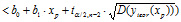=1-alfa

Таким образом, доверительный интервал для гипотезы H₀: M(YiX=x_p) = betta₀ + betta_0*х_р имеет вид:

нижняя граница доверительного интервала

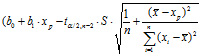
верхняя граница доверительного интервала

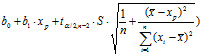
В доверительном интервале с надёжностью 1–alfa находятся значения зависимого фактора, лежащие на линии регрессии