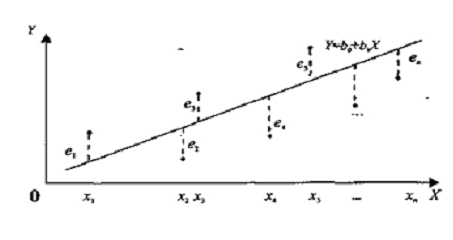
Задача линейного регрессионного анализа состоит в том, чтобы по конкретной выборке (xi, yi), i = l, 2, ... , n найти оценки a* и b* неизвестных параметров betta0 и betta1 так, чтобы построенная линия регрессии являлась бы наилучшей среди всех других прямых. Другими словами, построенная прямая yтеор(xi) = a* + b*•xi должна быть “ближайшей” к точкам наблюдений по их совокупности. Мерами качества найденных оценок могут служить определенные композиции отклонений ei, i = 1, 2, ... , n.
Существует несколько методов нахождения коэффициентов a* и b* эмпирического уравнения регрессии. Самым распространенным и теоретически обоснованным является метод наименьших квадратов (МНК).
При использовании данного метода минимизируется следующая функция (рисунок — изображение отклонений, сумма квадратов которых минимизируется):

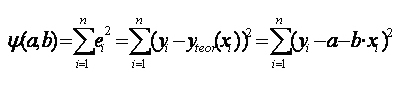
Функция psi является квадратичной функцией двух параметров a и b (psi = psi (a, b)), поскольку (xi, yi), i = 1, 2, … , n — известные данные наблюдений. Так как функция psi непрерывна, выпукла и ограничена снизу (psi > 0), то она имеет минимум.
Необходимым условием существования минимума функции двух переменных является равенство нулю ее частных производных по неизвестным параметрам a и b:
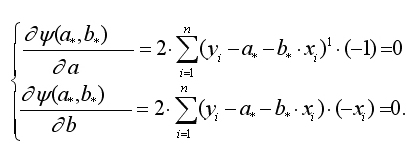
Это система нормальных уравнений.
После удаления 2 и (-1) (они не равны нулю) и приведения подобных получим:
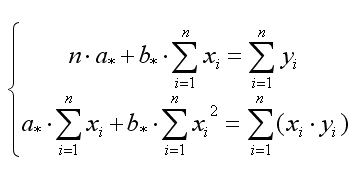
Выразим a* в первом уравнении через b*
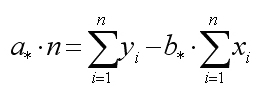
или
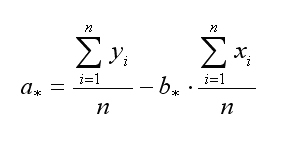
или по-другому,
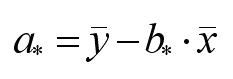

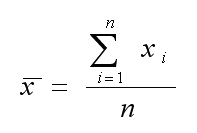
Подставив выражение (*) во второе уравнение системы, получим:
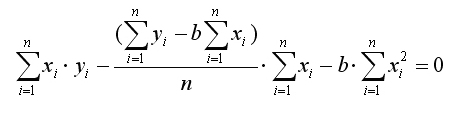
Тогда
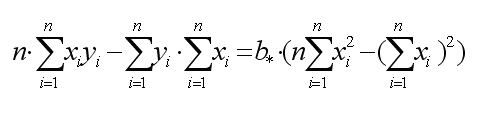
Таким образом,
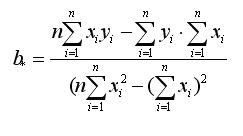
или

Теперь благодаря выражениям (*) и (**) имеем выборочное уравнение линейной регрессии:
yтеор (xi) = a* + b*xi,
Таким образом, по МНК оценки параметров a* и b* определяются по формулам (*), (**).