Эконометрика : 5.Оценка значимости коэффициентов парной линейной регрессии и экономической модели в целом.

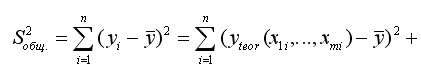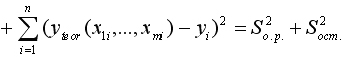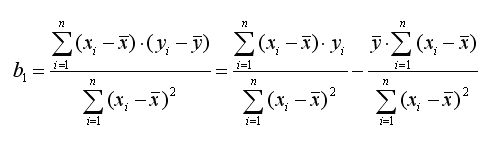
Представим формулы определения коэффициентов b0 и b1 в виде линейных функций относительно значений Y:

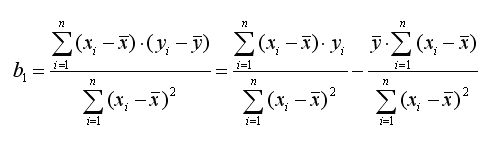
Отсюда

так как

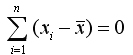
Введя обозначение

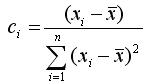
имеем:

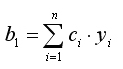(8.1)

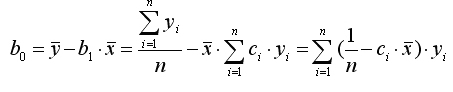
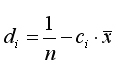
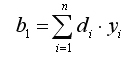(8.2)

Так как предполагается, что дисперсия Y постоянна и не зависит от значений X, то сi и di можно рассматривать как некоторые постоянные. Следовательно,

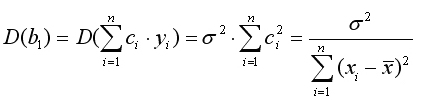(8.3)

и,

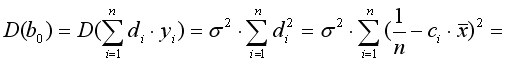
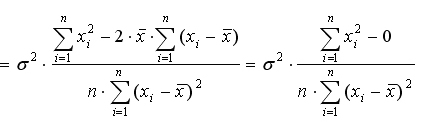
Таким образом,

D (b0)=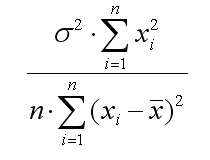(8.4)

Из соотношений (8.3), (8.4) очевидны следующие выводы.

• Дисперсии b0 и b1 прямо пропорциональны дисперсии случайного отклонения Ню2 зависимой переменной Y. Следовательно, чем больше фактор случайности по переменной Y, тем менее точными будут оценки.

• Чем больше число n наблюдений, тем меньше дисперсии оценок. Это вполне логично, так как чем большим числом данных мы располагаем, тем вероятнее получение более точных оценок.

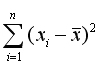• Чем больше дисперсия (разброс значений) объясняющей переменной X, тем меньше дисперсия оценок коэффициентов. Другими словами, чем шире область изменений объясняющей переменной, тем точнее будут оценки (тем меньше доля случайности в их определении).

В силу того, что случайные отклонения epsiloni по выборке определены быть не могут, при анализе надежности оценок коэффициентов регрессии они заменяются отклонениями ei = yi — b0 — b1xi значений yi переменной Y от оцененной линии регрессии. Дисперсия случайных отклонений D (epsiloni) = Ню2 заменяется ее несмещенной оценкой

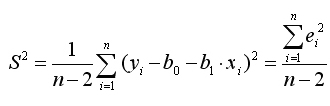(8.5)

Тогда

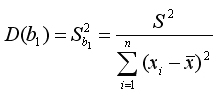(8.6)

(8.7)

Здесь

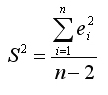
Это необъясненная дисперсия (мера разброса зависимой переменной вокруг линии регрессии). Отметим, что корень квадратный из необъясненной дисперсии, т. е.

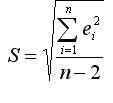
называется стандартной ошибкой оценки (стандартной ошибкой регрессии).

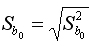
и

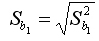
Это стандартные отклонения случайных величин b0 и b1, называемые стандартными ошибками коэффициентов регрессии.

Поскольку полагается, что betta1 = 0, то формально значимость оцененного коэффициента регрессии b1 проверяется с помощью анализа отношения его величины к его стандартной ошибке

При выполнении исходных предпосылок модели эта дробь имеет распределение Стьюдента с числом степеней свободы Ню = n-2, где n — число наблюдений. Данное отношение называется t-статистикой:

(8.10)

Для t-статистики проверяется нулевая гипотеза о равенстве ее нулю. Очевидно, t = 0 равнозначно b1 = 0, поскольку t пропорциональна b1. Фактически это свидетельствует об отсутствии линейной связи между X и У.

По аналогичной схеме на основе t-статистики проверяется гипотеза о статистической значимости коэффициента b0:

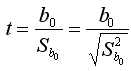(8.11)

Проверка значимости всего уравнения регрессии в целом
После оценки индивидуальной статистической значимости каждого из коэффициентов регрессии обычно анализируется совокупная значимость коэффициентов, т. е. всего уравнения в целом. Такой анализ осуществляется на основе проверки гипотезы об общей значимости гипотезы об одновременном равенстве нулю всех коэффициентов регрессии при объясняющих переменных:

H0: betta1 = betta2 = … = bettam = 0.

Если данная гипотеза не отклоняется, то делается вывод о том, что совокупное влияние всех m объясняющих переменных Х1, Х2, …, Хm модели на зависимую переменную Y можно считать статистически несущественным, а общее качество уравнения регрессии — невысоким.

Проверка данной гипотезы осуществляется на основе дисперсионного анализа сравнения объясненной и остаточной дисперсии.

Н0: (объясненная дисперсия) = (остаточная дисперсия),
H1: (объясненная дисперсия) > (остаточная дисперсия).

Строится F-статистика:

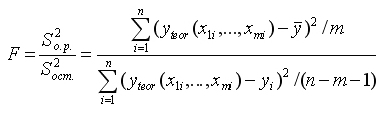(8.19)

где

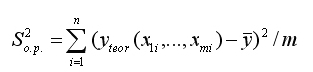
Это объясненная регрессией дисперсия;

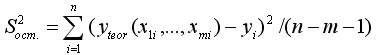
Это остаточная дисперсия (сумма квадратов отклонений, поделённая на число степеней свободы n-m-1). При выполнении предпосылок МНК построенная F-статистика имеет распределение Фишера с числами степеней свободы Ню1 = m, Ню2 = n-m-1. Поэтому, если при требуемом уровне значимости alfa Fнабл > Falfa; m; n-m-1 = Falfa (где Falfa; m; n-m-1 — критическая точка распределения Фишера), то Н0 отклоняется в пользу Н1. Это означает, что объяснённая регрессией дисперсия существенно больше остаточной дисперсии, а следовательно, уравнение регрессии достаточно качественно отражает динамику изменения зависимой переменной Y. Если Fнабл < Falfa; m; n-m-1 = Fкр., то нет основания для отклонения Н0. Значит, объясненная дисперсия соизмерима с дисперсией, вызванной случайными факторами. Это дает основание считать, что совокупное влияние объясняющих переменных модели несущественно, а следовательно, общее качество модели невысоко.

Однако на практике чаще вместо указанной гипотезы проверяют тесно связанную с ней гипотезу о статистической значимости коэффициента детерминации R2:

Н0: R2 = 0,
Н0: R2 > 0.

Для проверки данной гипотезы используется следующая F-статистика:

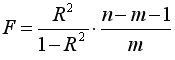(8.20)

Величина F при выполнении предпосылок МНК и при справедливости H0 имеет распределение Фишера, аналогичное распределению F-статистики (8.19).