Эконометрика : 6.Модель множественной линейной регрессии. Экономический смысл и оценка ее параметров.

Множественная регрессия — это уравнение статистической связи с несколькими независимыми переменными:

(5.1)

где y — зависимая переменная (результативный признак);

x1, x2, …, xp — независимые переменные (факторы). Все эти переменные входят в уравнение (5.1) с некоторыми коэффициентами. Метод наименьших квадратов (МНК) позволяет приближённо оценить значения этих коэффициентов.

Поведение некоторых экономических переменных контролировать нельзя, т. е. не удается обеспечить равенство всех прочих условий для оценки влияния одного исследуемого фактора. В этом случае следует попытаться выявить влияние других факторов, введя их в модель, т. е. построить уравнение множественной регрессии

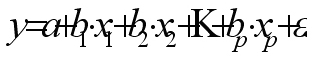
Такого рода уравнение может использоваться при изучении потребления. Тогда коэффициент bj — частные производные потребления y по соответствующим факторам xi:

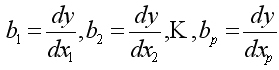
в предложении, что все остальные xi постоянны.

В линейной множественной регрессии коэффициенты при хi характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизменных значениях других факторов, закреплённых на среднем уровне.

При изучении вопросов потребления коэффициенты регрессии рассматриваются как характеристики предельной склонности к потреблению. Например, если функция потребления С_t имеет вид С_t = b₀ + b₁* R_t + b₂* R_t-1 +epsilon_t, то потребление за t-й период времени зависит от дохода того же периода R_t и от дохода предшествующего периода R_t-1. Соответственно, коэффициент b₁ характеризует эффект от единичного возрастания дохода R_t при неизменном уровне предыдущего дохода. Коэффициент b₁ обычно называют краткосрочной предельной склонностью к потреблению. Общим эффектом возрастания как текущего, так и предыдущего дохода будет рост потребления на величину b = b₁+b₂. Коэффициент b рассматривается здесь как долгосрочная предельная склонность к потреблению.

Функция потребления может рассматриваться также в зависимости от прошлых привычек потребления, т.е. от предыдущего уровня потребления C_t-1:

С_t = b₀ + b₁R_t + b₂C_t-1 + e_t.

В этом уравнении параметр b₁ также характеризует  краткосрочную предельную склонность к потреблению, т.е. влияние на потребление единичного роста доходов того же периода. Долгосрочная предельная склонность к потреблению имеет вид b₁/(1- b₂).

В степенной функции y_теор(x₁,x₂,…,x_p) = ax1^b1 x2 ^b2 …xp ^bp коэффициенты b1, b2, …, bp   являются коэффициентами эластичности. Они показывают, на сколько процентов изменяется в среднем результат с изменением соответствующего фактора на 1% при неизменности действия других факторов. Этот вид уравнения регрессии получил наибольшее распространение в производственных функциях, в исследованиях спроса и потребления.

Оценка коэффициентов уравнения множественной регрессии

Множественная регрессия широко используется в решении проблем спроса, доходности акций, при изучении функции издержек производства, в макроэкономических расчетах и целого ряда других вопросов эконометрики. В настоящее время множественная регрессия — один из наиболее распространенных методов в эконометрике. Основная цель множественной регрессии — построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также совокупное их воздействие на моделируемый показатель.

Параметры уравнения множественной регрессии оцениваются методом наименьших квадратов (МНК), 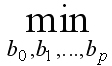т. е. минимизируется функция S (b0, b1,…, bp) по переменным b0, b1,…, bp

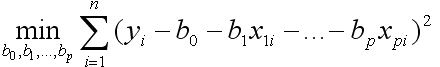S(b0, b1,…, bp) =(5.3)

На основании необходимого условия экстремума функции многих переменных S(b₀, b₁,..., b_p), представляющей (5.3), необходимо приравнять к нулю частные производные по этим переменным или в матричной форме — вектор частных производных

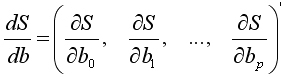
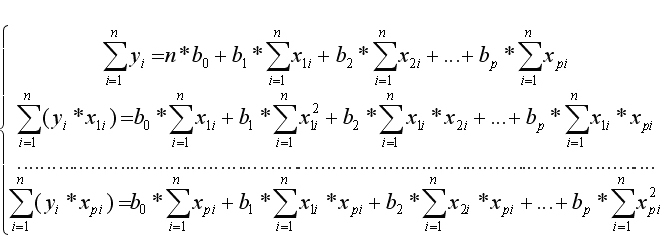
В результате получится система p+1 линейных уравнений для неизвестных b₀, b₁,..., b_p. После приведения подобных членов получится система нормальных уравнений, решение которой и позволяет получить оценку коэффициентов множественной регрессии.

Так для уравнения y_teor(x_1i, x_2i, ..., х_pi) = b₀+b₁x_1i + b₂x_2i +…+ b_px_pi система нормальных уравнений имеет вид: