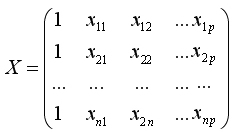
Обозначим
yi = betta0 + betta1×1i + betta2×2i +…+ bettapxpi+ epsiloni, (5.4)
где i = 1,2,…, n;
Модель (5.4) называется классической нормальной линейной моделью множественной регрессии (Classic Normal Linear Multiple Regression model).
Включение в регрессионную модель новых объясняющих переменных усложняет получаемые формулы и вычисления. Это приводит к целесообразности использования матричных обозначений. Матричное описание регрессии облегчает как теоретические концепции анализа, так и необходимые расчетные процедуры.
Введем обозначения:
Y=(y1, y2,…,yn)' —
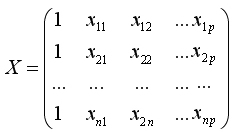
Это матрица значений объясняющих переменных, или матрица плана размера nх (p+1) (обращаем внимание на то, что в матрицу X дополнительно введен столбец, все элементы которого равны 1,
betta = (betta1, betta2,…,bettan)' —
epsilon = (epsilon1, epsilon2,… epsilonn)' —
Тогда в матричной форме модель регрессии по генеральной совокупности (5.4) примет вид:
Y= Xbetta+epsilon. (5.5)
Оценкой (приближением) этой модели по выборке является уравнение
Y=Xb+e, (5.5')
где b = (b0, b1,…,bp), е = (е1, е2,…,. еn)'.
Для оценки вектора неизвестных параметров betta применим метод наименьших квадратов. Так как произведение транспонированного вектора е' на сам вектор е равно
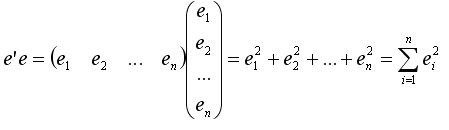
то условие минимизации остаточной суммы квадратов запишется в виде:
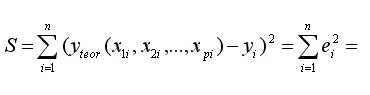
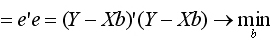 (5.6)
(5.6)
Учитывая, что при транспонировании произведения матриц получается произведение транспонированных матриц, взятых в обратном порядке,
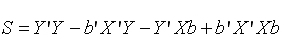
Произведение Y’Xb есть матрица размера (1хn)[nх (p+1)]х [(p+l)xl]=(lxl),
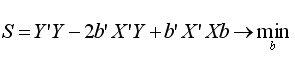
На основании необходимого условия экстремума функции нескольких переменных S (b0, b1,…, bp), представляющей (5.6), необходимо приравнять нулю частные производные по этим переменным или в матричной форме — вектор частных производных
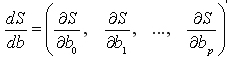
Для вектора частных производных в курсе высшей математики доказаны следующие формулы:
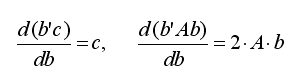
где b и с —
Справедливость приведенных формул проиллюстрируем на примере.
Пример 1. Пусть
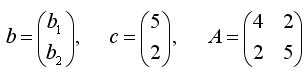
Так как
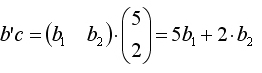
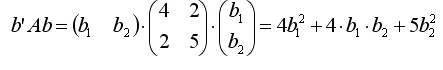
то
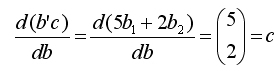
и
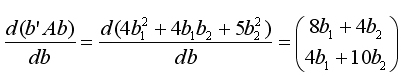
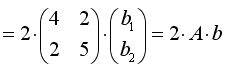
Поэтому, полагая с = X'Y, а матрицу А = X'•X (она является симметрической), найдем
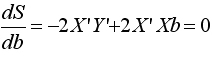
откуда получаем систему нормальных уравнений в матричной форме для определения вектора b:
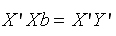 (5.8)
(5.8)
Найдем матрицы, входящие в это уравнение. (Здесь под знаком SUM подразумевается  ).
).
Матрица А = Х'Х представляет матрицу сумм первых степеней, квадратов и попарных произведений n наблюдений объясняющих переменных:
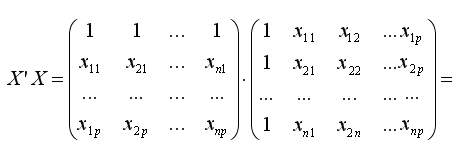
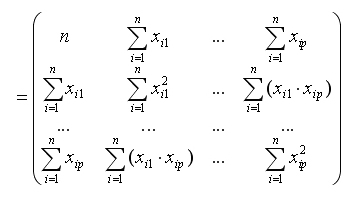
Матрица X'Y есть вектор произведений n наблюдений объясняющих и зависимой переменных:
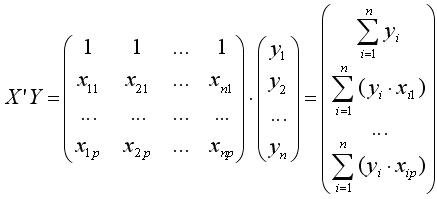
В частном случае из рассматриваемого матричного уравнения (5.8) с учетом (5.9) и (5.10) для одной объясняющей переменной (р = 1) нетрудно получить систему нормальных уравнений. Действительно, в этом случае матричное уравнение (5.8) принимает вид:
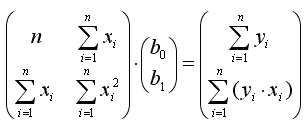
откуда непосредственно следует система нормальных уравнений для парной линейной регрессии.