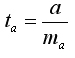Эконометрика : 8.Дисперсионный анализ. Суть и методика его расчета.

Дисперсионный анализ позволяет выявить взаимосвязи между исследуемыми переменными, то есть определить влияние отдельных факторов на переменную y.

На основе дисперсионного анализа можно рассчитать F-критерий Фишера и оценить значимость уравнения в целом.

Dобщ=Dфакт+Dост

Центральное место в нём занимает разложение общей суммы квадратов отклонений переменной у от среднего значения на две части — «объяснённую» и «необъяснённую»:

Sобщ=Sфакт+Sост

Здесь

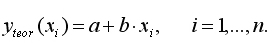
Любая сумма квадратов связана с числом степеней свободы (df — degrees of freedom), с числом свободы независимого варьирования признака. Число степеней свободы связано с числом единиц совокупности n и с числом определяемых по ней констант.

Существует равенство между числом степеней свободы общей, факторной и остаточной суммой квадратов отклонений. Число степеней свободы остаточной суммы квадратов при линейной регрессии составляет n-2. Число степеней свободы общей суммы квадратов определяется числом единиц варьируемых признаков, и поскольку мы используем среднюю вычисленную по данным выборки, то теряем одну степень свободы, т. е. dfобщ. = n-1

n-1 = 1+(n-2)

Разделив каждую сумму квадратов на соответствующее ей число степеней свободы, получим средний квадрат отклонений, или, что то же самое, дисперсию на одну степень свободы D.

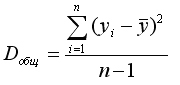
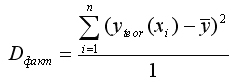
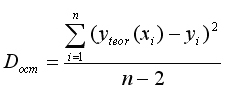
Определение дисперсии на одну степень свободы приводит дисперсии к сравнимому виду. Сопоставляя факторную и остаточную дисперсии в расчёте на одну степень свободы, получим величину F-критерия Фишера

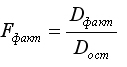
где F-критерий для проверки нулевой гипотезы H0: Dфакт = Dост.

Если Fфакт> Fтабл, то модель значимая
Если Fфакт< Fтабл, то модель не значимая, то есть x никак не влияет на y. (b=0)

Величина F-критерия связана с коэффициентом детерминации

Факторную сумму квадратов отклонений можно представить как

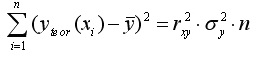
а остаточную сумму квадратов – как

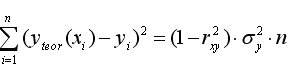
Тогда значение F-критерия можно выразить как

В линейной регрессии обычно оценивается значимость не только уравнения в целом, но и отдельных его параметров. С этой целью по каждому из его параметров определяется его стандартная ошибка: mb и ma.

Стандартная ошибка mb коэффициента регрессии b, определяется по формуле

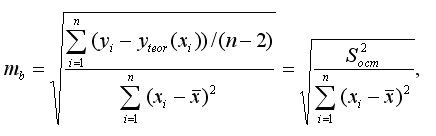
где

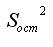
это остаточная дисперсия Dост на одну степень свободы.

Стандартная ошибка коэффициента регрессии a определяется по формуле

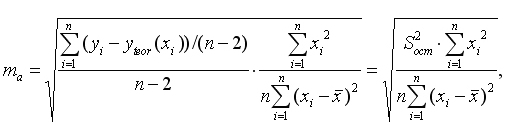
Где

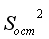
это остаточная дисперсия Dост на одну степень свободы.

Процедура оценивания существенности данного параметра, а такая же, как и для параметра b: вычисляется t-критерий