ЭММ : 11.Сведение игры к задаче линейного программирования(только этот взят со шпор, остальное с лекций). Итерационный метод Брауна-Робинсона

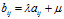
Для решения сложных матричных игр (m, n>2) разработан сравнительно простой метод решения, который заключается в сведении матричной игры к задаче линейного программирования, которая, в свою очередь, может быть решена хорошо известными методами (например, симплекс-методом) или с помощью многочисленных инструментов компьютерного моделирования (например, «Поиск решения» Excel). Как впервые показал Дж. фон Нейман (создатель теории игр и изобретатель симплекс-метода): любая конечная игра двух лиц с нулевой суммой может быть представлена как задача линейного программирования.

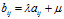
Аффинное правило. Оптимальные стратегии матричных игр, А и В, элементы платежных матриц которых связаны равенством

i=1,m j=1,n, где λ>0, a μ — любое вещественное число, имеют одинаковые равновесные ситуации (либо в чистых, либо в смешанных стратегиях), а цены игр удовлетворяют следующему условию: Ub= λ Ua+μ.

Пусть имеем матричную игру с матрицей, А порядка m x n. Предположим, что цена игры положительна (υ>0). Если это не так, то согласно аффинному правилу всегда можно подобрать такое число μ, прибавление которого ко всем элементам матрицы выигрышей даёт матрицу с положительными элементами, и, следовательно, с положительным значением цены игры. При этом оптимальные смешанные стратегии обоих игроков не изменяются.

Из определения оптимальной смешанной стратегии следует, что игрок 1, придерживающийся своей оптимальной смешанной стратегии «выиграет» не меньше υ при любых стратегиях игрока 2 {в т. ч. чистых), а игрок 2. придерживающийся своей оптимальной смешанной стратегии «проиграет» не больше υ при любых стратегиях игрока 1 (в т. ч. чистых).

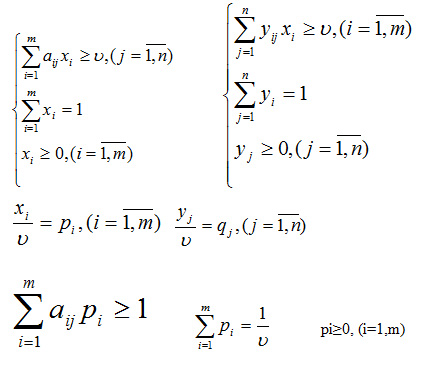
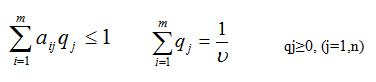
Поскольку первый игрок стремится максимизировать цену игры ? выбором значений xi, то обратная величина 1/ ? должна минимизироваться выбором рi

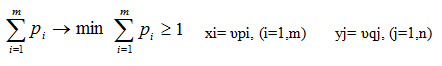
Поскольку второй игрок стремится найти такие значении уj и, следовательно, qj, чтобы цена игры сбыла наименьшей, то решение второй задачи сводится к нахождению таких неотрицательных значений qj, при которых

Решение любой матричной игры может быть осуществлено приведением игры к задаче линейного программирования и решением пары двойственных задач. Однако это требует большого объёма вычислений, которое растёт с увеличением числа чистых стратегий игроков (Например, для матрицы 33 имеем систему из 6 неравенств и 2 уравнений).

Поэтому в первую очередь следует, используя метод исключения доминируемых стратегий, уменьшить число чистых стратегий игроков (Исключение не строго доминируемых стратегий может привести к потере некоторых решений. Если же исключаются только строго доминируемые стратегии, то множество решений игры не изменится).

Затем следует проверить наличие Седловой точки. Если в игре есть Седловая точка, то игроки имеют чистые оптимальные стратегии, и решение получается автоматически.

В противном случае хотя бы у одного игрока оптимальные стратегии будут смешанные. Для простых матричных игр, где хотя бы у одного из игроков имеется только 2 стратегии, могут применяться аналитические и графические методы решения. Для более сложных игр необходимо использовать метод приведения игры к задаче линейного программирования.

Итерационный метод Брауна-Робинсона

В ряде случаев более целесообразным является отыскание решения матричных игр не методом приведения к 2-м ЗЛП, а другими методами, обеспечивающими менее точное решение, но являющиеся более простыми и не требующими громоздких вычислений. Наибольшее распространение среди матричных игр получил метод Брауна-Робинсон который основан на «мыслительном эксперименте», где игроки многократно разыгрывают игру и пытаются выявить те стратегии, которые дают им больший накопленный выигрыш. Одно разыгрывание игры — партия. Число партий может быть сколько угодно большим. Данный процесс также называется итерационным, поскольку в каждой партии (итерации) игроки используют один и тот же алгоритм выбора наилучшей стратегии.

Итерации метода предст-ся в виде таблицы

К — номер партии (итерации)
I — чистые стратегии игрока, А
В1, В2, …, Вn — накопленный выигрыш игрока A при чистых стратегиях B
ύ1 (k) — аналог нижней цены игры (ύ1 (k) = min (В1, В2, …, Вn)/k)
J — чистая стратегия игрока В
A1, A2, …, An — копленный проигрыш игрока A при стратегиях игрока B
ύ2 (k) — аналог верхней цены игры (ύ2 (k) = max (A1, A2, …, An)/k)
ύ(k) — аналог цены игры (ύ(k) = (ύ1 (k) + ύ2 (k)) / 2)

Оптимальные смешанные стратегии игроков определяются частотами выбора чистых стратегий, а в качестве цены игры применяют значение Ню, полученное на последнем шаге.

Данный итерационный процесс сходится, т. е. с ростом числа итераций точность решения увеличивается и после достаточного числа итераций можно получить решение с заданной точностью, но скорость сходимости довольна мала. Т. е. для получения оптимальных стратегий часто необходимо провести 10 или 100 операций. Однако сложность и объем вычислений сравнительно слабо возрастают по мере увеличения числа стратегий игроков.

Для определенности считают, что первый ход делает игрок, А и выбирает свою осторожную стратегию.

Если несколько стратегий игрока дают один и тот же результат, то с т.з. его накопленного выигрыша (проигрыша) выбирается стратегия с меньшим номер.

Оптимальные стратегии игроков определяются частотами выбора их чистых стратегий. Приближенное значение цены игры — результатом ύ(k) на последней итерации.

	maxmin	Ua(j)				minmax	Ua(i)
K	i	1	2	3	Ню1	j	1	2	Ню2	Ню
1	1	2	0	3	0/1	2	0	3	3/1	1,5
2	2	3	3	0	0/2	3	3	0	3/2	0,75
И.т.д.