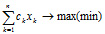
Линейные модели являются одним из наиболее активно используемых классов мат. моделей. Они сравнительно просты и хорошо разработаны, допускают полное исследование и достаточно эффективны в целом ряде стандартных ситуаций.
Программирование в данном термине имеет смысл планирования, а линейное означает, что ищется экстремум линейной целевой функции при линейных ограничениях.
Целевая функция:
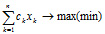
Ограничения:
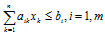
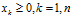
Исходя из сложности задачи можно решить (оптимизировать) ее одним из доступных методов.
Однако как только условия, в соответствии с которыми была построена модель, изменяются, то информация, связанная с оптимальным решением теряет актуальность. Анализ модели на чувствительность связан с исследованием возможных изменений полученного оптимального решения в результате изменения исходной модели.
Конечный результат анализа модели на чувствительность — это ответ на вопрос «изменится ли ранее полученное оптимальное решение?», если да, то каково новое.
Возможны 2 варианта: полученное решение может стать недопустимым или неоптимальным.
К недопустимости могут привести: — изменение правых частей ограничений; — введение новых ограничений.
Введение нового ограничения, в свою очередь, также приводит к одной из двух ситуаций: — новое ограничение при текущем решении не выполняется, поэтому необходимо найти новое решение; — новое огр. выполняется и не изменит решения. В любом случае, введение новых ограничений не может улучшить результат.
Что касается оптимальности, то решение перестает быть оптимальным только в том случае, когда новое значение
Общая схема анализа модели на чувствительность:
Таким образом, результаты, полученные при анализе модели на чувствительность можно сформулировать следующим образом: