Пример
|
8 |
5 |
3 |
|
2 |
3 |
6 |
8×1 + 2×2 => sum
5×1 + 3×2 => sum
3×1 + 6×2 => sum
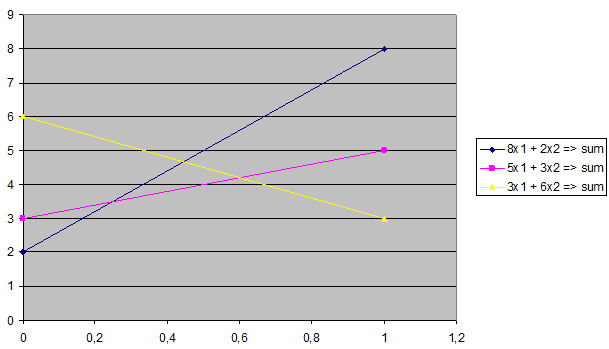
5×1 + 3×2 = sum
3×1 + 6×2 = sum
X = (x1, x2) x2 = (1 — x1)
x1 = 3/5
x2 = 2/5
Sum = 4 1/5
В играх с нулевой суммой общая сумма всех выигрышей равна нулю,
Игры такого класса с двумя игроками называются антагонистическими, или матричными,
Матричные игры решаются на основе писсиместического критерия: каждый из игроков стремиться сделать как можно хуже другому. Этот критерий оптимальности реализуется в поиске равновесия в осторожных стратегиях,
Ню1 = maxmin aij — нижняя цена игры, показывает какой выигрыш может гарантировать себе игрок, А при всевозможных стратегиях игрока В. Ню2= minmax aij — верхняя цена игры, показывает какой максимальный платеж получит, А, если Б выбирет свою осторожную стратегию. Если ню1 = ню2, то в игре существует устойчивое равновесие в осторожных стратегиях.
В этом случае говорят, что в игре существует седловая точка и игра решается в чистых стратегиях.
Если элемент матрицы является минимальным в строке и максимальным в столбце, то такой элемент называется седловым, а его координаты соответствует седловой точке.
Игра не имеющая Седловой точки называется неполностью определенной, в ней исходом игры является распределение разницы
Смешанная
Смешанная
Числа хi и yj можно интерпретировать как вероятности стратегии Ai первым игроком и Bj вторым игроком соответственно.
Теорема фон Неймана — любая матричная игра с нулевой суммой имеет решение в
Для любой матричной игры есть стретег ситуация, где определяется x0,y0 и для которой определяется условия Неша: Ua (x,y0)<=Ua (x0,y0)<=Ua (x0,y), где x и y произвольные смешанные стратегии игроков, А и В соответственно. Платеж, А в точке
Рассмотрим простейший случай матрицы 2*2:
а11 а12
а21 а22
Пусть x=(x1,x2)- оптимальные смешанные стратегии игрока, А, y=(y1,y2)- оптимальные смешанные стратегии игрока B.y2=1-y1 , x2=1-x1 .
Решение игры для игрока, А определяется след си:
при y1=1, y2=0: a11*x1*1+a12*x1*0+a21*(1-x1 )*1+a22*(1-x1 )*0>=Ню
при y1=0, y2=1: a11*x1*0+a12*x1*1+a21*(1-x1 )*0+a22*(1-x1 )*1>=Ню
Отсюда найдем х=(х1,х2) и Ню
Решение игры для игрока B определяется след си:
при х1=1, х2=0: a11*y1*1+a12*(1-y1 )*1+a21*y1*0+a22*(1-y1 )*0>=Ню
при х1=0, х2=1: a11*y1*0+a12*(1-y1 )*0+a21*y1*1+a22*(1-y1 )*1>=Ню
Отсюда найдем y=(y1,y2) и Ню
Графоаналитический метод решения игр:
Отыскивается оптимальная стратегия игрока с двумя чистыми стратегиями (предварительно исключаются все доминируемые стратегии и проводится проверка на наличие Седловой точки).
Считается, что этот игрок выбирает свою оптимальную стратегию, а его противник перебирает свои чистые стратегии.
Полученная система неравенств решается графическим методом. На графике строится ломанная, которая характеризует нижнюю границу (минимальный платеж, А) находится точка равновесия (максимальная точка на ломанной), определение координат которой дает оптимальную стратегию одного игрока и цену игры.
Затем определяется оптимальная стратегия другого игрока путем решения системы уравнения двух прямых, проходящих через точку равновесия.
Игра m*2 (m стратегий игрока, А и 2 стратегии игрока В) решается аналогичным образом, но
Пример
8
5
3
2
3
6
8×1 + 2×2 => sum
5×1 + 3×2 => sum
3×1 + 6×2 => sum
5×1 + 3×2 = sum
3×1 + 6×2 = sumX = (x1, x2) x2 = (1 — x1)
x1 = 3/5
x2 = 2/5
Sum = 4 1/5