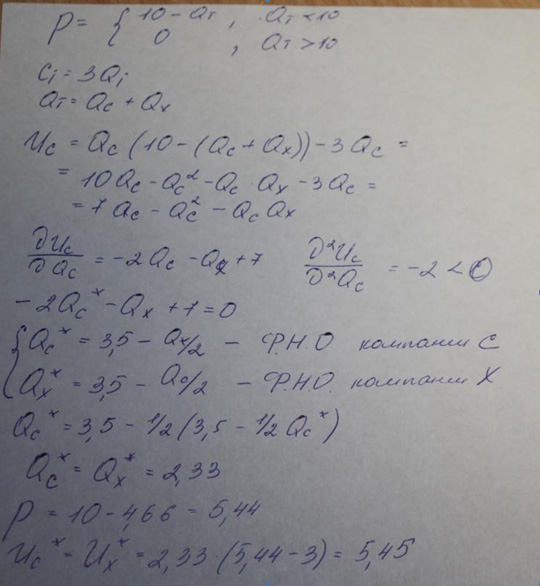Игры с непрерывными стратегиями — игры, в которых платежи игроков задаются с помощью функции Ui=fi (x1…xn),
В ряде случаев использование модели игры с непрерывными стратегиями может значительно упростить анализ конфликтной ситуации.
Однако в отличии матричн и биматричных игр не всякая игра с непрерывными стратегиями
Наиболее простой механизм решения стат игр с непрерывн стратег существует для
Если f (x;y)-дважды непрерывно дифференцируемая
df/dx=(x*,y)=0
df/dx=(x,y*)=0. Эта же система позволяет найти ФНО для каждого из игроков.
Пример: две компании Серебряный источник, А и Хрустальный источник В предлагают на дуаполистическом рынке миниральную воду и определяют объем поставок Qa, Qb соответственно. Общее предложение на воду определяет цену. Товар считается аналогичным по качеству. Технологические условия таковы, что обе компании д/заключить договор с поставщиками,
ч/б удовлетворить спрос. После подписания контрактов изменение объема поставки не возможно. Определить оптимальные стратегии.
Известно, что рыночная цена
p=10-Qт , если Qn<10 и
0, если Qт>=10.
Удельные затраты компаний Ci=3Qi.
Прибыль каждой компании Ui (Qa,Qd)= (10-(Qa+Qd))Qi-3Qa , если Qa+Qb<10, или = -3Qi, если Qa+Qb>=10
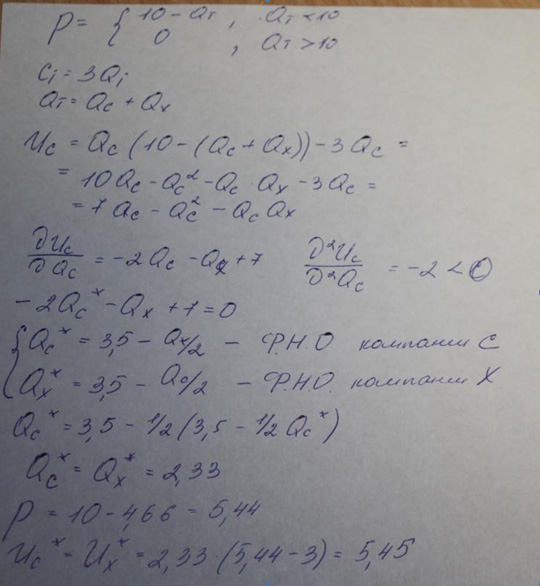
Биматричные игры — конечная игра двух игроков, которая полностью определяется двумя платежными матрицами.
Ua=знак суммы по m знак суммы по n AijXiYj, Ub=знак суммы по m знак суммы по n BijXiYj
Условие равновесия по Нэша для биматричных игр (кто отклоняется тому хуже):
Ua (x,y*)<=Ua (x*,y*)
Ub (x*,y)<=Ub (x*,y*)
Условие равновесия для биматричной игры должно выполняться в том числе для любых стратегий игроков xi, y,. Тогда получаем си неравенств:
Ua (xi,y*)<=Ua (x*,y*), i=1….n
Ub (x*,yj)<=Ub (x*,y*), j=1….n
Любая биматричная игра имеет решение в чистых или смешанных стратегиях (т. Нэша)
Общий принцип решения биматричных игр.
В первое неравенство системы последовательно подставляются все чистые стратегии игрока, А, при предположении, что В придерживается своей оптимальной стратегии.
Во второе неравенство подставляются все чистые стратегии игрока В, при предположении, что, А придерживается своей оптимальной стратегии.
Полученная сситема m+n неравенств, решение которой дает значение элементов оптимальных смешанных стратегий (x*,y*) и платежи, получаемые игроками в точке равновесия.
Пример: борьба за рынок.
А = -10 2 В = 5 -2
1 -1 -1 1
Равновесия в чистых стратегиях нет.
ПЕРВЫЙ ВАРИАНТ
Ua=-10×1y1+2×1 (
Ub=5×
Пусть
x1=1-> Ua=
x1=0->Ua=-1+2y1<=-14×1y1+3×1+
y1=1->Ub=-1+6×1<=9×
y1=0->Ub=1–3×1<=9×
составляем 4 системы ,преобразовываем, получаем:
(
x1 (-14y1+3)>=0
(
y1 (9×1–2)>=0
х1=0-> -(-14y1+3)>=0 y1>=3/14
х1=1-> (-14y1+3)>=0 y1<=3/14
0<x1<1-> -(-14y1+3)>=0 и (-14y1+3)>=0->y1=3/14
y1=0->x1<=2/9
y1=1->x1>=2/9
0<y1<
Строим график по всем x и всем y, получается на пересечении точка x1=2/9, y1=3/
X=(2/9;7/9), Y=(3/14;11/14)
Ua=-4/7, Ub=1/3
Вывод: 2/9 товара предлагать на первом рынке и 7/9 на втором рынке и тогда минимал проигрыш — 4/7. 3/14 -защищать
-4/7-> ему вообще не выгодно выходить на рынок, но если для него это приемлемая цена, то ему надо действовать именно так, иначе он отступит от своей оптимальной стратегии и ему будет хуже.
ВТОРОЙ ВАРИАНТ
Решение биматричной игры путем её декомпозиции
Те же матрицы, А и В.
Решение игры, представляемой матрицей, А:
-10×1+(
2×1-(
x1=2/14, ню=-4/7
-10y1+2 (
y1-(
y1=3/14, ню=-4/7
Решение игры,
X=(2/9;7/9), y=(1/3;2/3) ню=1/3.
Решение исходной биматричной игры для игрока, А совпадают с решением для игрока, А игры,
Решение исходной биматричной игры для игрока В совпадают с решением для игрока В игры,
Платеж игрока, А в точке равновесия, полученной при решении исходной биматричной игры, совпадает с ценой матричной игры, задаваемой платеж матриц игрока А.(и то же самое для В)
Следовательно, модель биматричной игры подразумевает, что принимая решение о выборе оптимальных стратегий, каждый из игроков стремиться отслеживать и контролировать действия др игрока.
